
In this section we will present the numerical schemes with which the steady states and the stability of these were computed. Most of the numerical analysis on the steady states were performed with Mathematica@. The results were checked by numerical integration of the pde model (Eqs. 10-16) with the escalator box car train method [10].
The central equation in computing the steady-states will be
Using Eq. (26), Eq. (34) can be rewritten as
In steady-state we can think of the population size in a patch being originated from growth in an undisturbed patch, i.e. population size can be obtained by solving the ode
![]()
Using this relation we can rewrite the integral in Eq. (35) as a fictive age integral
Combing Eqs. (20, 23, and 26)
we can write ![]() as
as
When we only allow total disasters, i.e. ![]() , the nasty integral containing
, the nasty integral containing ![]() disappears in both Eqs. (36 and 37), and
disappears in both Eqs. (36 and 37), and ![]() is the only quantity to be determined. In this case the integrals on the
rhs. of (36) are computed by simultaneously solving the
following set of ode's
is the only quantity to be determined. In this case the integrals on the
rhs. of (36) are computed by simultaneously solving the
following set of ode's
up to the age at which ![]() is sufficiently close to
zero. A secant method is then used to find the root of equation (36).
is sufficiently close to
zero. A secant method is then used to find the root of equation (36).
If the disasters are partial, both ![]() and the steady-state density
distribution
and the steady-state density
distribution ![]() are unknown. It turned out that the following
iterative scheme converged slowly, to stable steady states. Instead of using
Eq. ( 26) as a substitute for
are unknown. It turned out that the following
iterative scheme converged slowly, to stable steady states. Instead of using
Eq. ( 26) as a substitute for ![]() we computed
we computed ![]() from the ode
from the ode
in which ![]() is the maximum attainable local
population size obtained by solving
is the maximum attainable local
population size obtained by solving ![]() . In the iterative
scheme we started with an initial guess of
. In the iterative
scheme we started with an initial guess of ![]() , then we computed a
starting distribution
, then we computed a
starting distribution ![]() by solving Eq. (42) with
by solving Eq. (42) with ![]() . Next we computed from
. Next we computed from ![]() a lookup table for
a lookup table for
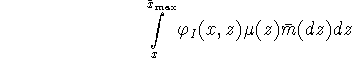
and a new value of ![]() by solving the ode's
by solving the ode's
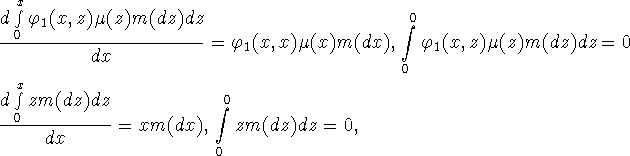
In the subsequent steps we computed a new distribution and ![]() by
using Eq. (42) with the lookup table from the previous iteration.
The iteration process was stopped when the subsequent
by
using Eq. (42) with the lookup table from the previous iteration.
The iteration process was stopped when the subsequent ![]() 's were
sufficiently close. We were not able to find unstable steady states in this
way.
's were
sufficiently close. We were not able to find unstable steady states in this
way.
To compute the dominant eigenvalue ![]() from the characteristic
equations (Eqs 45-46) we used the same procedure
as in the computation of the steady states in case of total disasters. Again
we change to fictive patch age, and build a system of
from the characteristic
equations (Eqs 45-46) we used the same procedure
as in the computation of the steady states in case of total disasters. Again
we change to fictive patch age, and build a system of ![]() -dependent ode's to solve with
-dependent ode's to solve with ![]() , given a lookup table for
, given a lookup table for ![]() . The secant method is used again to find the dominant real root of
Eqs. (45-46).
. The secant method is used again to find the dominant real root of
Eqs. (45-46).