In this section we will derive the characteristic equation from which the
stability of the equilibria (Eqs. 22-24) of the
metapopulation model (Eqs. 19-21) can be determined.
To do so we first linearize system (Eqs. 19-21)
around b and 
. Thereafter we insert an exponential trial
solution, which directly gives the wanted equation.
For the linearization define the deviations from the steady states as
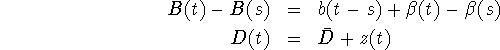
Substitution in (Eqs. 19-21) and Taylor expansion up to first order results in
and
If we now insert the exponential trial solution
define 
, and 
, and
use the fact that 
are only dependent
on D through x, we get the characteristic equations
and,
in which
are quantities still left to be computed. If we define
and follow the derivations laid out in appendix C, then (Eqs. 47,49,50) are computed from the differential equations
in which
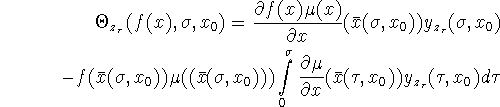
The initial conditions for these ode's are
Equation (52) can be solved resulting in
Now Eq. (48) can be written as
If 
is constant and if there are only total
disasters, then 
and the linearized equations simplify to
an uncoupled system of characteristic equations: one equation for the patch
dynamics
which has dominant eigenvalue 
, and therefore the
steady-state age distribution is neutrally stable, and another equation for
the population living on this neutrally stable distribution
