For a determination of the fate of a metapopulation we have to analyze the
stability of the size (or age) distribution of the patches, the disperser
density and the fraction of unsuitable patches in steady state. In the
following, steady states will be denoted by a bar. Before concentrating on
some specific realizations of v(x) and ![]() we derive some general
results.
we derive some general
results.
The steady state disperser density is obtained by putting Eq. (3) equal to zero. We get
From Eq. (20) we obtain the steady state fraction of empty patches
At last, the steady state age distribution is given by
in which ![]() is the solution of Eq. (2) starting from
is the solution of Eq. (2) starting from ![]() with density
with density ![]() , and experiencing the steady
state disperser density
, and experiencing the steady
state disperser density ![]() on the interval [0,t].
on the interval [0,t].
Due to conservation of patches the steady state age distribution must satisfy
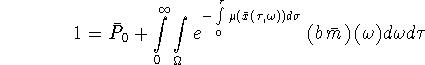
and so
Equations (1,22, 23, and 25), should provide the means for calculating the actual steady state values. For computational convenience however, we determined the steady states numerically using Eqs. (1,22, and 25), in combination with the steady state size distribution
which was obtained after integration of Eq.(10) (see appendix A for the numerical scheme).
The asymptotic behavior around the steady state is dependent on the value
of the dominant eigenvalue ![]() of the resolvent of Eqs. (19-21). In appendix B, Eqs. (45-46), the
characteristic equation is given from which the dominant eigenvalue is
computed.
of the resolvent of Eqs. (19-21). In appendix B, Eqs. (45-46), the
characteristic equation is given from which the dominant eigenvalue is
computed.
Equation (24) provides us the steady age distribution: the distribution of patch lifetimes between two consecutive disasters. In a field situation one would be more interested in the mean lifetime of a patch before it is struck by a disaster wiping out the whole population, which is given by the equation