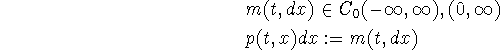
In this paragraph we will concentrate on measures for which
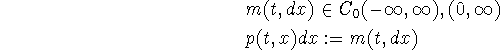
Note that because of Eq. (1) p(t,x) can be regarded as the (defective) probability distribution of patches over local population density x.
Following Metz & Diekmann [9] we can represent the metapopulation dynamics by the forward Kolmogorov functional partial differential equation
for which we must define a boundary condition at x=0.
When total disasters may occur, i.e. 
, empty patches
are formed at a rate
When a total disaster does not result in a loss of habitat quality, the patch will be re-colonized by dispersers instantly. The resulting boundary condition is
which simply states that the flux into habitable patches of zero
population size is the same as the rate of total disasters. A result of
habitat quality being unaffected by total disasters is that there can be no
empty patches. This is in contrast to what was assumed by Gyllenberg &
Hanski [4]. In their model, patches hit by a total disaster are set aside
in a pool of empty patches ( 
), instead of contributing to the pool of
suitable patches. Colonization of empty patches, at the arbitrarily level x=1, happens due to the law of mass action involving dispersers and empty
patches. The rate of change in the fraction of empty patches is then
resulting in the boundary condition
which is dependent on the density of dispersers.
Suppose now that there is a probability u that after a total disaster a
patch becomes unsuitable for habitation, and that the time required to
regain habitat quality is taken from an exponential distribution with
parameter 
, we then get
and
independent of D.
This is just a simple model describing habitat recovery. More complex models
might require the incorporation of an age distribution of empty patches. The
resulting model will certainly be different from the model of Gyllenberg &
Hanski, except for the case where the size of the instream of dispersers
affects the recovery of habitat, i.e. is a function of D.
The problem becomes well posed if we specify the initial conditions. For ease of reference we repeat the full model
