Levins [8] introduced the concept of a metapopulation with the continuous-time patch-occupancy model
where 
is the set of possible equilibria. In this model
empty patches are
infected by occupied patches due to mass action,
and local extinction is a random event independent of the metapopulation
state. Extinction and migration are processes at a time scale exceeding that
of local dynamics. Hanski [7] tried to make migration act on a faster
time scale by assuming a rescue effect on patch extinction, leading
heuristically to the model
Both the Levins and Hanski models require m;SPMgt;e for a non-trivial equilibrium. Due to our assumption that migration is such a frequent event that it influences local dynamics, empty patches do not exist in our model unless they are unsuitable for habitation. Therefore the adjustment to the Levins model made by Hanski can only be valid if habitat becomes unsuitable after a disaster.
Gotelli [3] argued that re-colonization might be due to migration out of a mainland, resulting in the model
This model does not have a trivial equilibrium unless m=0. Note
that this system resembles an open system for population size. Since in our
model habitat recovery is independent of dispersers, re-colonization is
described by 
which is similar to 
in the Gotelli
model. However, in our model re-colonization is part of a closed system, and
reflects habitat recovery instead of migration from an external pool.
Patch-occupancy is influenced by the metapopulation through the extinction
rate 
only. In case is constant, equation (29) for 
is exactly that of Gotelli. However, it only gives information
about habitat quality, and none about the state of the species living in it.
The existence of a viable population then depends on the dynamics of the
local populations on a random pattern of suitable habitat patches. If a
population exist then is indeed the fraction of occupied patches.
In many field experiments a positive relation between 
and is found.
Does our model lead to this conclusion? To answer this question we simplify the model
further by assuming, as in the Hanski [7] model, that the dynamics on patch
level and
disperser level are faster than the extinction dynamics, and such fast
that the local population is in steady-state, i.e. let v(x) be such that 
, 
for some 
. Then all habitable patches will have density 
, and 
, with 
the Dirac delta
function. This results in
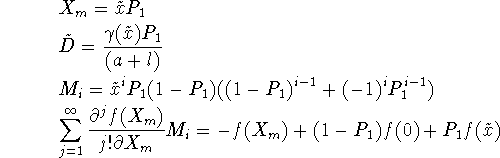
and so the equation for patch occupancy based on fast local dynamics becomes
in which is computed from
With this simple model we can deal analytically with the relation between
occupancy and population size. The steady-state values, and , are fully determined by the parameters and their directional
changes are given by the equations
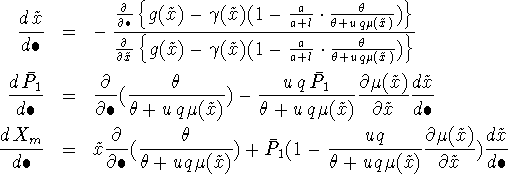
Whenever is an increasing function of x, the directional change
of and are opposite. An increase in does
not necessarily result in an increase of patch occupancy and mean population
size , and might increase while is decreasing. If is a decreasing function of x, both patch occupancy and mean
population size are increased. Since many field experiments show a positive
relation between and our model indicates that these natural
populations behave as model 
, a disaster model put forward to
mimic extinction due to demographic stochasticity.
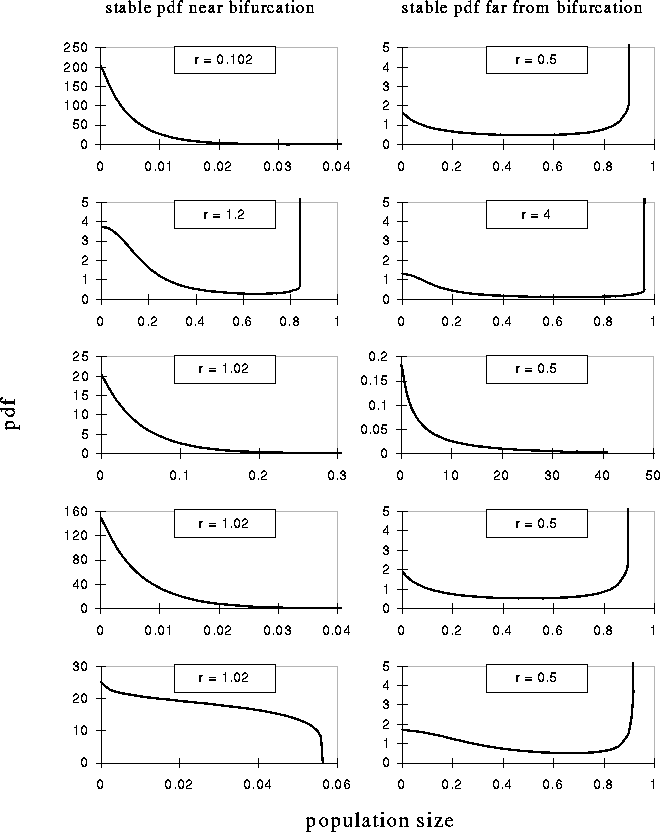
Figure 6: Probability density functions of unsafe (near bifurcation)
(left picture) and safe (far from bifurcation) (right picture)
meta-populations for the models in fig.1a-5a.
The assumption that empty patches are unsuitable for habitation is put in
the model rather artificially in order to mimic a Levins-type model, in a
situation where empty patches are impossible due to a high migration
pressure. Let us return to the full model and suppose that patches are
always habitable. Our model then bears a result equivalent to the
migration-extinction balance of the Levins model. If the difference in time
scale between the local dynamics and extinction is enlarged (Levins: m
increased relative to e, our model: r increased relative to 
), the
fraction of high density patches is increased (fig. 6). So, if we consider
patches with a density smaller than an arbitrary small number as empty (cf.
[5]), the fraction of empty patches becomes smaller if either the
extinction rate is decreased or the local dynamics increased (fig. 7).
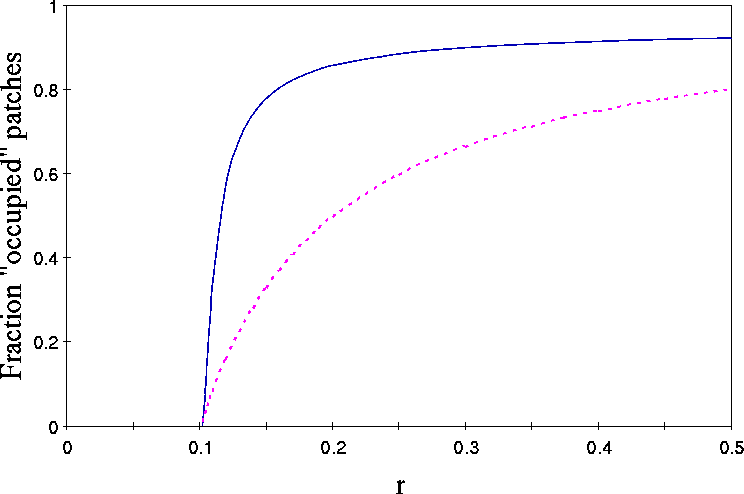
Figure 7: Solid line: Fraction of patches above detection threshold
0.025 for example (II,i,a,q=1). Parametervalues as in fig. 1a. Dashed
line: Fraction of occupied patches in the Levins (1970) model 1-e/m
redefined as 
.
Another analogy is found in the requirements for the existence of a non-trivial equilibrium. In the Levins model it is required that colonization exceeds extinction, i.e. m;SPMgt;e . In our model the trivial equilibrium is unstable when at low density the net per capita reproduction within a patch exceeds extinction (Eq. (28)), i.e. in the case of logistic growth and any extinction rate from our examples,
In other words, at low densities the patch extinction rate is equal to the death rate of an individual, and migration can only take place when population density can grow away from zero locally.